Optimization and Lagrange Multipliers
[\require{cancel}]
Optimization
Suppose, you want to buy a car. but you are a bit confused which one to buy as there are alot of options… but your mathematician wife knows you pretty well and she quickly constructed this preference function for you which tells you which car you’ll prefer and which car you don’t according to the looks or features of the car…
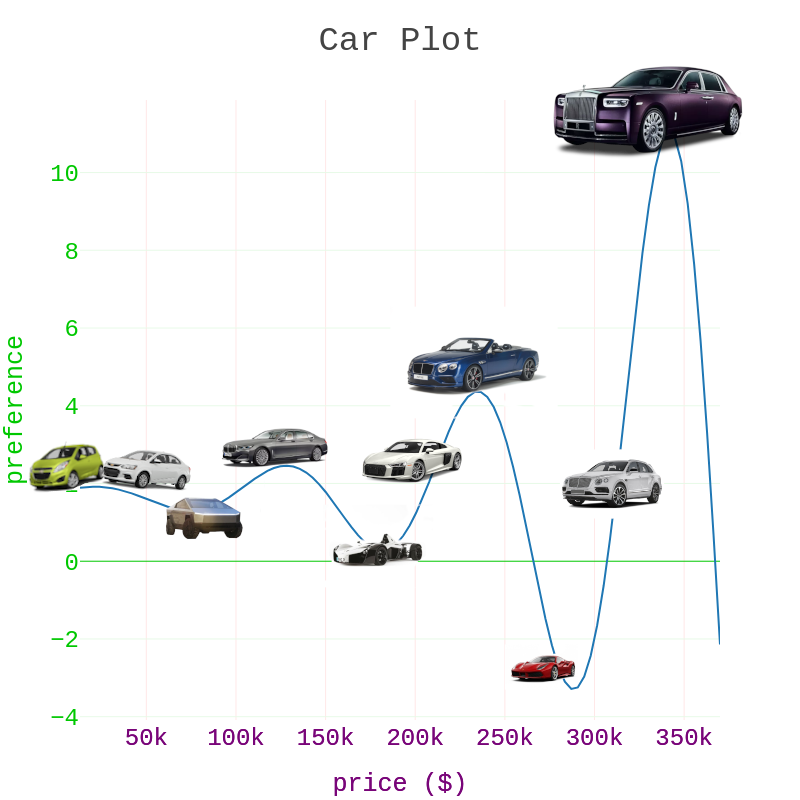
Fig 1: Car Plot :- here, the 'x'-axis represents the price of the car and 'y'-axis denotes your preference for a particular car.
As you can see, this function is non-linear(not a straight line) which makes sense because there might be some cars who’s price is high but you did’nt like its design or maybe you are looking for a family car or something…
now, if you have infinit budget then you don’t even have to look at the price of the car, you can just choose a car with the highest preference value.. soo go ahead and find the best possible car by adjusting the slider below..
Fig 2: find the best car by tweaking that slider on the left
So, the line you just adjusted is called a contour line. A contour line of a function is a set of all points where the output of our function is equal to a constant i.e, \(f(x) = c\)… like in our case, when we adjust the contour line we essentially set \(f(x) = c\) in-which we adjusted the value of c by moving that slider (as you can see in that red box at the bottom of the slider)… which gave us the set of all the cars whose preference function value is equal to \(c\).
Now that you have found which car you want to buy, you head back to you wife again and unsurprisingly the conversation goes something like this:
ME: hey, thankyou for that pereference function earlier, i finally know which car i am gonna buy
Wife: Oh that awesome, how much does it cost?
ME: its half a million
Wife: half a... what!!... what are you Bill Gates or something?
After that “friendly” conversation with you wife, she gave you the budget and 2 bumps on your head.
You see, in real life we almost always have some constraints which we need to follow and try to find the best possible values of our function without volating these constraints.
So, you went back to your graph viz thingy and plot the function along with the feasible region a.k.a the region of the cars you can afford (denoted in orange color below) :
Fig 3: this plot shows the range of car we can afford in orange along with the usual preference function values..
now, the orange highlighted section of our preference function curve represent the preference value of the cars which you can afford(f(feasible points)). which means, now you need to find the best possible value while remaining within this constraint region… so you take that contour line again and search for the best possible value of your preference function but this time instead of searching for any car you like regrardless of the price, here, we restrict ourselves to only look for the best possible car which are in our budget ( coz ya would’nt wanna mess with ya wife again..)
Fig 4: tweak the slider and try to find the best possible value which are still in your budget..
now, that you have found the best car which is still in your budget you went back to your wife with this result and guess what, she liked it too!
What you just did above (by manually searching for the best possible car without violating your constraints) is exactly the reason why we need optimimzation for.
Imagine instead of a 1 dimensional function, you have a 10 or a 100 dimensional function ( for example, in this case suppose the openion/preference of the entire family matter not just yours. here, you can image a function with 5-6 dimensions each representing the preference function of all the members of the family)… you can’t possibly be thinking of finding the optimal values manually right? that is where optimization comes in. its just a mathematical framework which can give you the most optimal value provided our functions and our constraints(if any).
Now before moving forward, lets make ourselves a bit familier with some of the termonologies(a.k.a mathematical jargon) used in this field…
-
so, that preference function in our earlier example, is known as objective function… because our objective was to find the maximum value of that function right?
-
the process by which we are finding the best possible value of our objective function without violating the constraints(if any) is known as optimization.. its same as adjusting that contour line…
-
if we don’t have any constraint its known as unconstriant optimization
-
after performing optimization, the best value we get is known as optimal value and the best point is known as optimal point like in fig 3, our optimal value is
2.459and our optimal point is128.40kwhich is just the price of our most prefered car. -
points which satisfy all of our constraints are known as feasible points like those point that are highlighted in orange (see fig 3)
Lagrange Multipliers
In order to solidify our understanding even further and to observe what is really happening when we optimize a higher dimensional function not just a 1d function (like we saw before) lets look at one more example before looking at the mathematical framework of finding these optimal values..
Suppose, you have variables \(x_1\) and \(x_2\) and a function \(f\) which takes this 2 variables as input and spits out a single value (mathematically we write this statement as \(f: R^2 -> R\)) for e.g. let \(f(x_1,x_2) = x_1 + x_2\) and let \(x_1 = 2\) and \(x_2 = 3\) then \(f(2,3) = 5\)…this type of function is known as multi-variate function for obvious reasons
In context of our car example in the previous section, we can think of \(x_:w\) as fuel consumption of the car maybe?
Anyways, in this example we are going to be using a multivariate function:-
[f(x_1,x_2) = x_1^2 + x_2^2 \tag{1}]
along with the equality constraint:-
[\begin{align}
g(x_1,x_2) &= 2x_1 + 3x_2 = 20
{} &= 2x_1 + 3x_2 -20 \tag{2}
\end{align}]
if we plot our objective function as well as our constraint region, it will look something like this:-
Fig 5: this plot shows our objective function in (blue) and our constraint region and there corresponding objective function values in (orange)
Now lets look at our final plot below. here, just like before, we can easily find the best feasible minimum value (as oppose to finding the maximum value ) by adjusting our contour line slider but here, along with the objective function,constraint and our contour line…we have also shown the feasible points within our contour line \(f(x'_1,x'_2) = c,\) where, \(x'_1,x'_2\) are feasible points represented by those gray dots…\ In the right-hand side plot, we have also, shown the gradient vector of the function as well as the gradient vector of constraint evalued at each of these gray points..Although, these information may seem overwhelming at first but the observation we get by playing with these plots will help us greatly in constructing our mathematical formulation for automatically detecting our optimal points which we can then use to find the optimal value/points of any function with equality constriants(i.e, \(g(x_1,x_2) = 20\) in our case) in any number dimensions..
ASIDE:
Fig 6: (left) along with the usual things we saw in the previous figure this one also shows the feasible points that are in our contour line ( we call them contour feasible points which are represented by gray dots ), we have also shown the global minimum point just for reference.
(right) here, we have shown the cross-section/slice of our objective function which is made by our contour line and along with our contour feasible points we have also shown the gradient of our objective function as well as our constraint function.
while adjusting the contour line we can clearly see that when we get closer and closer to the minimum value while still satisfying our constriants. the gradient of both the objective function and constraint function of those contour feasible points , points at almost the same directions! and at the optimal point these gradient vectors points at exactly the same direction and differ only by there magnitude!…
we can leverage this observation to construct the mathematical equivalent of searching for optimal points i.e,…
Mathematically, at optimal point, the gradient vector of the objective function points to the same direction as the gradient vector of the constraint function and differ only by a scaling factor…
[\nabla f = \lambda \nabla g]
[f_{x_1}(\star{x}1, \star{x}_2) = \lambda g{x_1}(\star{x}_1, \star{x}_2)]
[f_{x_2}(\star{x}1, \star{x}_2) = \lambda g{x_2}(\star{x}_1, \star{x}_2)]
where, \((\star{x}_1, \star{x}_2)\) are the coordinates of our optimal point and \(f_x\) is the derivative of function w.r.t \(x\) and \(f_y\) is the derivative of the function w.r.t \(y\) respectively…
that scaling factor \(\lambda\) is known as the lagrange multiplier.
Now, lets use this discovery to find the optimal point for this optimization problem without manually searching them..
here, our objective function is:
[f(x_1,x_2) = x_1^2 + x_2^2 \tag{1}]
and our constraint function:-
[g(x_1,x_2) = 3x_1 + 2x_2 -20 \tag{2}]
and if we follow the textbook version of formulating an optimization problem it will look something like this:-
[\begin{array}
\min{}_{x_1,x_2}&{f(x_1,x_2) = x_1^2 + x_2^2}
\operatorname{subject to}&{g(x_1,x_2) = 3x_1 + 2x_2 -20 = 0}
\end{array}]
don’t worry, i know it looks a bit scary, but there is nothing here that we haven’t looked before.
Let’s break it down!
the first line
[\min{}_{x_1,x_2}\quad f(x_1,x_2)= x_1^2 + x_2^2]
simply means that we want to minimize our objective function with respect to \(x_1\) and \(x_2\), we can think of it as manually searching for those points \(x_1\) and \(x_2\) which when gets inserted into our function \(f(x_1,x_2)\) it produces the minimum possible value… (its simple, just pause and ponder :D )
Now, if we optimize just this first line we get the global minimum point from fig 6 because till this point we haven’t introduced any contraints just like we saw in our first example where we were trying to find the best car without caring about the budget, and what have we learned from our expericence back there? in real life there are almost always going to be constaints which we need to satisfy. which is exactly what is written in the second line of this optimization problem formulation….
[\operatorname{subject to}\quad{g(x_1,x_2) = 3x_1 + 2x_2 -20 = 0}]
here, our \(x_1\) and \(x_2\) are subject to our constaint function… I always like to imagine 2 points \(\bar{x}_1\) and \(\bar{x}_2\) (from our domain) go to a courtroom and are subjected to the question of the judge like do you satisfy this constraint or not or in our case, its going to be judge: do you \(\bar{x}_1\) and \(\bar{x}_2\) combine in this form see (2) and equal to 0? if both answers yes! then they both are considered for minimizing our objective function but
if one of them say no then these \(\bar{x}_1\) and \(\bar{x}_2\) are not even considered for the job and said to be infeasible for the rest of the there life….
sorry for that dark story (i am listening to heavy metal while writing this blog post :P) but I hope this will somewhat reduce your stress of seeing these weird mathematical symbols.
Solving using CODE
Instead of solving the optimization problem by hand we let computer do that work for us…
here, we will use a python library which solves our optimization problem for free… you just have to define your problem and thats it! it will automatically find optimal point as well as value for you ;D
# constructing our optimization problem using cvxpy
import cvxpy as cp
def f(x_1,x_2):
return x_1**2 + x_2**2
# initializing variables
x_1 = cp.Variable()
x_2 = cp.Variable()
#our objective
obj_fn = cp.Minimize(f(x_1, x_2))
# constraints
constraints = [3*x_1 + 2*x_2 -20 == 0]
# solving our optimization problem.
opt_prob = cp.Problem(obj_fn, constraints)
opt_prob.solve()
# printing important informations
print('status: ', opt_prob.status)
print('optimal function value', opt_prob.value)
print('optimal x_1 point', x_1.value)
print('optimal x_2 point', x_2.value)
>> status: optimal
>> optimal function value 30.769230769230766
>> optimal x_1 point 4.615384615384615
>> optimal x_2 point 3.0769230769230775
Now, if you had enough math for the day and don’t want any more of this weird language with weird symbols you can go ahead and skip the rest of the sections because now you know intuitively understand what lagrange multipliers are! and also know a bit about using CODE to solve our optimization problem!
but if your brain is still reeking for more maths then please, by all means, head over to our final section in which we are going to be solving our optimization problem by hand…
Solving by hand
Now, in order to find our optimal point it needs to satisfy 2 things,
-
our constraints: \(g(x_1,x_2) = 3x_1 + 2x_2 - 20 = 0 \tag{3}\)
-
as well as our previous observation i.e,
[\nabla f(x_1,x_2) = \lambda \nabla g(x_1,x_2) \tag{4}]
which for our exmple means:
[\nabla{f} =
\left [
\begin{matrix}
f_{x_1}
f_{x_2}
\end{matrix}
\right ]
=\left [
\begin{matrix}
2x_1
2x_2
\end{matrix}
\right ]]
and the gradient vector of the constraint function =>
[\nabla{g} =
\left [
\begin{matrix}
g_{x_1}
g_{x_2}
\end{matrix}
\right ]
=\left [
\begin{matrix}
3
2
\end{matrix}
\right ]]
putting these gradient vectors in \((4)\), we get:
[\nabla{f} = \lambda\nabla{g}]
[\left [
\begin{matrix}
2x_1
2x_2
\end{matrix}
\right ]
=
\lambda
\left [
\begin{matrix}
3
2
\end{matrix}
\right ]]
[\begin{align}
2x_1 &= \lambda3 \qquad{(5)}
2x_2 &= \lambda2 \qquad{(6)}
\end{align}]
we have 3 equations and three unknowns which mean we can easily solve this using standard algebric manipulations, which are as follows:
if we rearrange (5), we get:
[\begin{align}
2x_1 &= \lambda3
x_1 &= \frac{3\lambda}{2} \tag{7}
\end{align}]
if we re-arrange (6), we get:
[\begin{align}
2x_2 &= \lambda2
x_2 &= \frac{\cancel{2}\lambda}{\cancel{2}}
x_2 &= \lambda \tag{8}
\end{align}]
Now, putting both (7) and (8) in (3), we get the value of our \(\lambda\):-
[\begin{align}
3x_1 + 2x_2 - 20 &= 0
3 \left ( \frac{3\lambda}{2} \right ) + 2(\lambda) &= 20
\left ( \frac{9\lambda}{2} \right ) + 2(\lambda) &= 20
\left ( \frac{9\lambda + 4\lambda}{2} \right ) &= 20
\ 9\lambda + 4\lambda &= 2\times 20
13\lambda &= 40
\lambda &= \frac{40}{13} \qquad{(9)}
\end{align}]
using (9) we can finally calculate our (7) as well as (8) i.e,
[\begin{align}
x_1 &= \frac{3\lambda }{2}
x_1 &= \frac{3 \left ( \frac{40}{13} \right ) }{2} \qquad{(\text{using (9)})}
x_1 &= \frac{3 \times 40 }{2 \times 13}
x_1 &= \frac{120}{26} = \frac{\cancel{120}}{\cancel{26}} = \frac{60}{13} = 4.615 \qquad{(10)}
\end{align}]
Now, \(x_2\) is:
[\begin{align}
x_2 &= \lambda
x_2 &= \frac{40}{13} = 3.076\qquad{(\text{using 9})}\qquad{(11)}
\end{align}]
So, the point which minimize our objective function subjected to our constraint function is: (4.615, 3.076) and if we put this onto our objective function we get the most optimal value:-
[\begin{align}
f(x_1,x_2) &= x_1^2 + x_2^2
f(\left (\frac{60}{13} \right ),\left (\frac{40}{13} \right ))&= \left (\frac{60}{13} \right )^2 + \left (\frac{40}{13} \right )^2\quad{\text{(putting (10) and (11))}}
{} &= (4.615)^2 + (3.076)^2
{} &= 21.301 + 9.467
{} &= 30.769
\end{align}\]
So, in short, our optimal point is (4.615, 3.076), whereas, our optimal value is 30.769… which is exactly what we get if we manually toggle our contour line in fig 5 which means our math align 100% percent with our intuition!!.. which is quite beautiful don’t you think? ( please, let me know what you think about it)
Bonus
Now that we know everything there is to know about Lagrange Multipliers… we can look at a much more complicated visualization of lagrange multiplier:
here, instead of changing our function value using contour line we are running along the constraint region and moving over each of the feasible points and calculate there gradient vectors… Play with this visualization and see if you could figure out all the optimal points (hint: there are more then 1 optimal points :D ) you can also find the optimal points using the power of mathematics like we did in our previous section…
All the information regarding this visualization is in the description of this visualization
If you are able to reach here… then congratulations you have mastered the art of lagrange multipliers!!… you can now use this newly found knowledge to solve many world problems or you can extend this knowledge even further by learning more on optimization… here are some of the resource which i love and i am sure you will to :D
- https://christopherolah.wordpress.com/2011/07/31/you-already-know-calculus-derivatives/
- https://www.youtube.com/watch?v=WUvTyaaNkzM&list=PLZHQObOWTQDMsr9K-rj53DwVRMYO3t5Yr
- and for a more formal mathematical treatment i really like this resource:
- http://tutorial.math.lamar.edu/
- https://www.khanacademy.org/math/differential-calculus
- if you want to dive much deeper into optimization you can check out this classic and beautiful book :- https://web.stanford.edu/~boyd/cvxbook/
Anyways, i hope you enjoyed this post and learned something cool. if there is anything you want me to impove upon then please, feel free to tell me in the comment section below, i would really love to hear any critique or comments you might have!
Till then, Bye and Have a beautiful day ^_^

