Understanding Recurrent Neural Nets
Recurrent Neural Nets are one of the most crucial architecture to understand in the field of deep learning and for good reason, today, when it comes to modeling sequential data, our goto architecture are RNNs, whether it’s predicting what are you going to type next or to have a virtual assistant like Siri or Alexa or even to pridict stock prices.in-short,RNNs are important.
Now that you are convinced! we can move forward into really understanding it, don’t worry its not that unfamiliar…. it’s just a simple Neural-net including aspects of a dynamic system that are incorporated into its architecture with a twist in its backpropagation algorithm… so let’s get into it!
As discussed before, RNNs are used to model sequential data which are usually generated by a dynamic system like our speech, we can think of a dynamic system(see equation (1)) as a function which depends on the function of previous time step… i.e, when we deliver a sentence our choice of current word is bounded by the choice of our previous word and so on.. for example, we can’t just say “Today harry a beautiful day” instead of “Today is a beautiful day”…
[S_t = f(S_{t-1}) \tag{1}]
and if we were to represent it in computation graph it looks something like fig 1.1 (a):
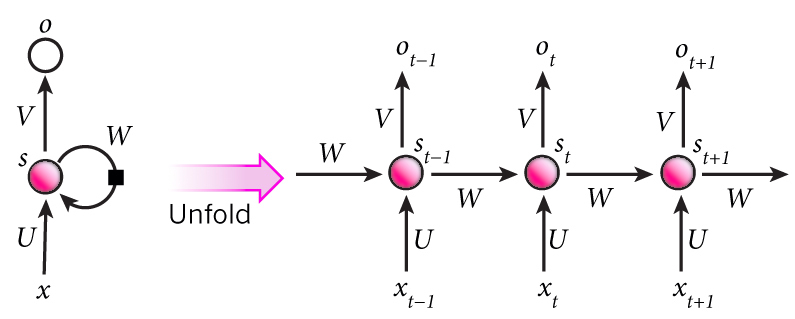 fig 1.1
a. Dynamic System (left) b. unfolded RNN graph (right)
fig 1.1
a. Dynamic System (left) b. unfolded RNN graph (right)
Some Notations to be aware of:-
- \(s_t\) = State or hidden units at time step \((t)\)
- \(o_t\) = output at time step (t)
- \(V\) = Weight Matrix b/w hidden unit and the output
- \(W\) = Weight Matrix b/w hidden units
- \(U\) = Weight Matrix b/w input and \(s_t\)
where,
[a_t = b + Ws_{t-1} + Ux_t]
\(s_t = \sigma(a_t)\) (where, \(\sigma\) = activation function )
[o_t = c + Vs_t]
now, in order to predict the next word or the next stock prices we first need to input some data and the way we are going to be doing that is by putting every input-unit(word in a sentence,history of stock prices) into each time step,think of it like our prior knowledge that we feed into our network in order to predict the next unit in the sequence…
in case of speech generation, the output is a huge matrix consist of the probabilities of occurence of every word in our vocabulary,in case of stock market prediction its going to be just a simple output of prices…. from now on we are just going to be focusing on the general form of a simple RNNs
ok, so we know how are we going to get our prediction but what if we predict it wrong?? first of all we need a measure to calculate the correctness of our prediction.enter, Loss function, loss function is just a accumulation of all the individual loss at each time step… i.e, \(l_t = 1/2*(o_t - y_t)^2\) where \(y_t\) is the true output and \(o_t\) is the probability @ timestep \(t\) although usually we use cross-entropy loss for language modelling but for simplicity we are going with standard MSE.
now that we know hot to quantify the correctness our prediction, we need to find a way to minimize it and just like a simple perceptron, we need to come up with Weights that minimize our Loss function. and the way we are going to be doing that is by calculating the derivative of our Loss function w.r.t. these weights which will tells us in which direction we should move in order to minimize our Loss function and update our weights accordingly. which means, we need to calculate these values:-
[{ {\partial L}\over{\partial V} }, { {\partial L}\over{\partial W} }, { {\partial L}\over{\partial U} } \tag{2}]
but in order to calculate these, we first need to calculate some derivatives beforehand,which will prove useful in calculating our final weight derivatives(2). first we need to calculate the derivative of \(o_t\) w.r.t our loss function:
[{ { \partial L }\over{\partial o_t}} = { { \partial L }\over{ \partial l_t }} * { { \partial l_t }\over{ \partial o_t } }]
so as we know:
[L = l_t + l_{t-1} + ….. + l_{1}]
[\begin{align}
{ { \partial L }\over{\partial l_t} } &= { {\partial }\over{\partial l_t} }(l_t + l_{t-1} + ……. + l_1)
&= 1
\end{align}]
for second term :
[\begin{align}
{ { \partial l_t } \over {\partial o_t} } &= {1\over2}({ {\partial } \over {\partial o_t} }((o_t - y_t)^2))
&= (o_t - y_t)*1
\end{align}]
putting it all together we get:
[{ { \partial L }\over {\partial o_t} } = { {(o_t-y_1)1}{1} }]
now the next thing we need to calculate is \({ {\partial L} \over{\partial s_t}}\), this is not an easy fleet… beacuse if you change \(s_t\) its going to change} \(s_{t+1}\) and} \(s_{t+2}\) and so on… untill the end of the time or untill the end of our input sequence and finally change our Loss function. so our derivative is going to be:
[{ {\partial L} \over{\partial s_t}} = ({ {\partial L} \over {\partial o_t} } * { {\partial o_t} \over {\partial s_t} }) + ({ {\partial L}\over{\partial s_{t+1}} } * { {\partial s_{t+1}}\over {\partial s_t} })]
for convenience, let \(\kappa = { {\partial L} \over{\partial s} }\)
[\kappa_t = ({ {\partial L} \over {\partial o_t} } * { {\partial o_t} \over {\partial s_t} } ) + (\kappa_{t+1} * ({ {\partial L}\over{\partial s_{t+1}} }*{ {\partial s_{t+1}}\over {\partial s_t} }) )]
where, \({ {\partial s_{t+1}}\over {\partial s_t} } = { {\partial }\over {\partial s_t} }(s_t*W) = W\)
but we can’t calculate \(\kappa_t\) just yet, basically we want to calcaulate the derivative w.r.t current time but as u can see in the expression above we also need to calculate the derivative w.r.t the next time step and so on…(because of \(\kappa_{t+1}\) ) untill the end of time…(litrally) that is why we first need to calculate the derivative w.r.t last time-step and then backpropagate through time to get to the current time step (t), which is the reason why this algorithm is known as backpropagation through time(BPTT).
so the derivative w.r.t last time step \((T)\) is going to be:
[{ {\partial L} \over{\partial s_T}} = { {\partial L} \over {\partial o_T} } * { {\partial o_T} \over {\partial s_T} }]
here, we know \({ {\partial L} \over {\partial o_T} }\)… but what about the second term??
[{ {\partial o_T} \over {\partial s_T} }={ {\partial} \over {\partial s_T} }(c + Vs_T) = V]
our final \({ {\partial L} \over{\partial s_T}}\) :-
[{ {\partial L} \over{\partial s_T}} = (o_t-y_t) * V]
it should be clear by now that the derivative of loss function w.r.t s_t is going to depend on the derivative w.r.t s_t+1 and s_t+2 and so on untill the last time step which we now know how to calculate, so our final expression of calculating \(\kappa_t\)
[\kappa_t = ( (o_t - y_t)* V) + ((\kappa_{t+1}) * W )]
[\kappa_{t+1} = ( (o_t - y_t)* V) + ((\kappa_{t+2}) * W )]
[\vdots]
[\kappa_{T-1} = ( (o_t - y_t)* V) + ((\kappa_{T}) * W )]
[\kappa_T = ( (o_t - y_t)* V)]
Finally we have every thing we need in order to calculate the derivatives our weights.. we can now move forward and calculate them respectively:-
[{ {\partial L} \over{\partial V}} = { {\partial L} \over{\partial o_t} } * { {\partial o_t} \over{\partial V} }]
[{ {\partial L} \over{\partial W}} = { {\partial L} \over{\partial s_t} } * { {\partial s_t} \over{\partial W} }]
[{ {\partial L} \over{\partial U}} = { {\partial L} \over{\partial s_t} } * { {\partial s_t} \over{\partial U} }]
calculating,\({ {\partial L} \over{\partial V}}\):
[\begin{align}
{ {\partial L} \over{\partial V}} &= { {\partial L} \over{\partial o_t} } * { {\partial o_t} \over{\partial V} }
&= (o_t - y_t) * { {\partial o_t} \over{\partial V} }
\end{align}]
[{ {\partial o_t} \over{\partial V} } = { {\partial} \over{\partial V} }(V*s_t) = s_t]
[{ {\partial L} \over{\partial V}} = (o_t - y_t) * s_t]
calculating,\({ {\partial L} \over{\partial U} }\):
[\begin{align}
{ {\partial L} \over{\partial U}} &= { {\partial L} \over{\partial s_t} } * { {\partial s_t} \over{\partial U} }
&= (\kappa_t) * { {\partial s_t} \over{\partial U} }
\end{align}]
[{ {\partial s_t} \over{\partial U} } = { {\partial s_t} \over{\partial a_t} }*{ {\partial a_t} \over{\partial U} }]
[{ {\partial s_t} \over{\partial a_t} } = { {\partial } \over{\partial a_t} }(tanh(a_t))]
[{ {\partial s_t} \over{\partial a_t} } = (1-tanh^2(a_t))]
[{ {\partial a_t} \over{\partial U} } = { {\partial } \over{\partial U} }(b+ Ws_{t-1} + Ux_t)]
[{ {\partial a_t} \over{\partial U} } = (x_t)]
[{ {\partial s_t} \over{\partial U} } = (1- tanh^2(a_t))*(x_t)]
[{ {\partial L} \over{\partial U}} = (\kappa_t)*((1-tanh^2(a_t)) * (x_{t}))]
calculating,\({ {\partial L} \over{\partial W}}\):
[\begin{align}
{ {\partial L} \over{\partial W}} &= { {\partial L} \over{\partial s_t} } * { {\partial s_t} \over{\partial W} }
&= (\kappa_t) * { {\partial s_t} \over{\partial W} }
\end{align}]
[{ {\partial s_t} \over{\partial W} } = { {\partial s_t} \over{\partial a_t} }*{ {\partial a_t} \over{\partial W} }]
[\begin{align}
{ {\partial a_t} \over{\partial W} } &= { {\partial } \over{\partial W} }(b+ Ws_{t-1} + Ux_i)
&= ( s_{t-1})
\end{align}]
[{ {\partial s_t} \over{\partial W} } = (1-tanh^2(a_t))* (s_{t-1})]
[{ {\partial L} \over{\partial W}} = (\kappa_t)*((1-tanh^2(a_t)) * (s_{t-1}))]
putting all the derivatives together our final derivative of Loss function w.r.t all the weights are:-
[{ {\partial L} \over{\partial V}} = (o_t - y_t) * s_t]
[{ {\partial L} \over{\partial U}} = (\kappa_t)*((1-tanh^2(a_t)) * (x_{t}))]
[{ {\partial L} \over{\partial W}} = (\kappa_t)*((1-tanh^2(a_t)) * (s_{t-1}))]
Now that we have the derivatives of all the weights we can finally compute our weights
[V_{\text{new}} = V_{\text{old}} + \alpha{ {\partial L} \over{\partial V} }]
[W_{\text{new}} = W_{\text{old}} + \alpha{ {\partial L} \over{\partial W} }]
[U_{\text{new}} = U_{\text{old}} + \alpha{ {\partial L} \over{\partial U} }]
Congratulations,now that you know how Recurrent Neural Network works internally/mathematically as well as intuitively…we can now worry about how to implement it… if you ask anyone in the industry they all say RNNs doesnt work as it is… in paper it is really great and this is how it works internall but in practice we need to do some modification in order to make it work and that we will do in the next part of this blog…
